
家庭教師が教える中学受験の算数
【市川中学編】
留意点1
6割を目標にしますが、今年は「難問揃いだ」と判断できれば5割を目標に。 重点を置くべき単元は「高難度な図形・グラフ」など。 市川中学の算数入試問題の試験時間50分。解答を書き入れる形式で、問題数は小問で15 問前後。 難易度は年によって変化しますが、年によっては序盤からとっつきにくい文章題や図形が 出ることもあるので、過去問への着手はなるべく早めに(遅くとも夏休み明け)。
留意点2
ここ最近は、「新傾向問題」や「典型問題に見せかけた揺さぶり問題」が数多く出題されて おり、過去問着手初期では、算数を得意とする受験生でも5割はおろか3、4割程度しか取 れないということも珍しくない為、過去問演習において「手を付ける順番」と「解いた後 の検証」にこだわる必要があります。
留意点3
この学校で最も注意すべきは「定規類禁止」ということで、「フリーハンド条件での作図問」 も数多く出題されているので、普段から平面でも立体でも積極的にノート等に図を写した り、あるいは「自分に都合の良い図にかきなおす」などの機転を利かす必要性がある
具体的な市川中学対策例
【注目の設問① H29 1-3】
35個のボールを、A、B、C、D、E、Fの6人でわけることになりました。まずAが7個もらい、A以外の5人は残りの28個のボールをとる順番をジャンケンで決め、勝った順に好きなだけとることにしました。全員がボールをとったあとに、A以外の5人に話を聞いたところ以下のように答えました。
5人の話
B:「残りの$2/3$をもらったよ」
C:「残りの$2/3$をもらったよ」
D:「残りの全部をもらったよ」
E:「残りの半分をもらったよ」
F:「Eより先にもらったよ」
6人がもらったボールの数はそれぞれ異なり、また、6人とも少なくとも1個はもらいました。このとき、上の5人の話からFは何個もらいましたか。
※一見「単純な割合の問題」に見えますが、実は「28個のボールをB~Fの5人がどのような順番で取ったかを推理する」という条件整理の面倒な問題です。
まず、すぐにわかることは、
① Dが最後にもらった
② BとCがもらうとき、それぞれ「3の倍数個」のボールが残っていた
③ Eがもらうとき、「偶数個」のボールが残っていた
①~③より、Aがもらったあと28個残っているので、このあとボールをもらうのはEかFですが、FがEより先にもらったので、28個からボールをもらうのはFということです。
そのあとにB、C、Eがいずれかの順番でボールをもらい、最後にDがもらうことになります。
(a) B→C→Eの順にもらうとすると、Eのときにボールは最低で2個残っている
(b) (a)より、Cがもらうときボールは最低 $2 \div (1-2/3)=6$ 個残っている
(c) (b)より、Bがもらうときにボールは最低 $6 \div (1-2/3)=18$ 個残っている
もしも(a)で、Eがとるときボールが $2×2=4$ 個残っていたとすると、(c)のときBがもらうボールが $18×2=36$ 個となり、28個を超えてしまうことから条件に合わなくなる為、Bがもらうときにボールは18個残っていたことになります。
(d) C→E→BやE→C→Bなどの順にもらう場合でも、Fの次にもらうときにボールは、
$3×2×3$$=3×3×2$$=18$ 個残っていることになります。
よってFがもらったボールの数は、$28-18=10$ 個であるとわかります。
※このように、この問題は「単純な割合の問題」ではなく「推理の問題」である為、冷静な条件整理の時間を要します。
このような問題は「一旦後回し」にし、試験時間後半でじっくり調べて確実に正解させるのがセオリーとなります。
【注目の設問② H30 1-6】
図1のように、長方形ABCDがあり、AB=8cm、AD=12cmです。点Pと点Sは、この長方形のたてを2等分、点Q、R、T、Uは、この長方形の横を3等分する点です。 ここで、図2のように長方形ABCDの内部に点Eをとり、EP、EQ、ES、ETを引いて、 長方形を4つの四角形に分けました。このとき、次の問いに答えなさい。
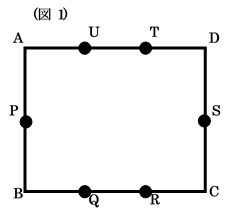
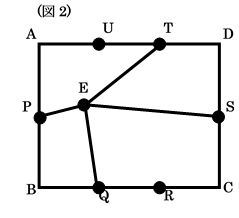
(1) 四角形ETAPと四角形EQCSの面積の和を求めなさい。(cm2)
(2) 四角形ETAPと四角形EPBQと四角形EQCSの面積の比が9:8:19のとき、四角形ESDTの面積を求めなさい。($cm^2$)
【解答解説】
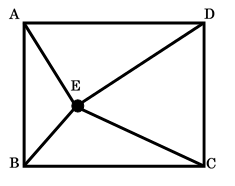
【基本性質】
(三角形$EAB$ の面積+三角形$ECD$ の面積)
$=$(三角形$EAD$の面積+三角形$EBC$の面積)
$=$長方形$ABCD$の面積$\times 1/2$
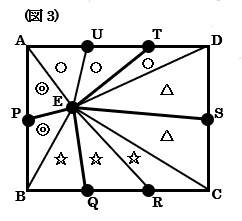
(1) 図3のように、点Eと点A、B、R、C、D、Uを直線で結びます。このとき、同じ印の三角形の面積(〇、◎、△、☆)どうしはすべて等しくなります。上の基本性質を利用すると、
$(〇〇〇)+(☆☆☆)$$=8×12÷2$$=48cm^2$より、$〇+☆$$=48\div3$$=16cm^2$ となります。
また、
$(◎◎)+(△△)$$=48cm^2$より、$◎+△$$=48\div2$$=24cm^2$となります。
よって、
四角形ETAPの面積+四角形EQCSの面積
$=(〇〇◎)+(☆☆△)$$=(〇+☆)×2+(◎+△)$$=16×2+24$$=56 cm^2$となります。
(2) 問題の条件と(1)の結果より、
四角形EPBQの面積:(四角形ETAPの面積+四角形EQCSの面積→($56cm^2$))
$=8:(9+19)$$=2:7$
四角形EPBQの面積$=56 \div 7 \times 2$$=16cm^2$となりますから、求める四角形ESDTの面積は、
$96-(56+16)$$=24cm^2$です。
※H30①6の最終大問である為、「(超)難問?かも」という先入観が生まれますが、意外にも「絶対死守すべき問題」ということになりますので、注意が必要です。
【注目の設問③ H27 1 (5)】
分数が並んでいる列に対して、次の操作をくり返し行います。
操作:となりあう分数の分子にかかれている数字どうし、分母にかかれている数字どうしをたして新しい分数をつくり、これを2つの分数の間に入れる。ただし、約分はしないものとする。
(例) 最初に与えられた分数の列が、$\frac{1}{6}, \frac{3}{4}$ のとき、
$\frac{1}{6}, \frac{3}{4}$
$\downharpoonright$
$\frac{1}{6},\frac{4}{10}, \frac{3}{4}$ (操作1回後)
$\downharpoonright$
$\frac{1}{6},\frac{5}{16},\frac{4}{10},\frac{7}{14}, \frac{3}{4}$ (操作2回後)
$\downharpoonright$
最初に与えられた分数の列が、$\frac{1}{2},\frac{1}{3}$ のとき、次の問いに答えなさい。
(1) 操作を4回行ったとき、右から7番目の分数を答えなさい。
(2) 操作を7回行ったとき、並んでいる分数の個数を答えなさい。
(3) 操作を8回行ったとき、並んでいる分数の分母にかかれている数字をすべてたすと いくつになるか答えなさい。
(1) (2)、(3)の問いを見越して、限られた試験時間で「どう動けばよいか」を判断する 必要があります。この問題のポイントは、以下の関係式に気づくかどうかです。
新しい分数の個数 = 操作前の分数の個数 - 1
となることから、
操作後の分数の個数 = 操作前の分数の個数 + 新しい分数の個数
⇒ 操作後の分数の個数 = 操作前の分数の個数 × 2 - 1
という関係が成り立ちます。これをふまえると、分数の個数は、
はじめ2個 → 操作1回で2×2-1=3個 → 操作2回で3×2-1=5個
→ 操作3回で5×2-1=9個 → 操作4回で9×2-1=17個
となります。
「右から7番目の分数」ということは、$17>7×2$$=14$より、
操作1回目でできる新しい分数$\frac{1+1}{2+3}=\frac{2}{5}$ より右側だけ調べればよいことがわかります。
操作1回目後 $\frac{2}{5}$, $\frac{1}{3}$
操作2回目後 $\frac{2}{5}$, $\frac{3}{8}$, $\frac{1}{3}$
操作3回目後 $\frac{2}{5}$,$\frac{5}{13}$,$\frac{3}{8}$,$\frac{4}{11}$,$\frac{1}{3}$
操作4回目後 $\frac{2}{5}$,$\frac{7}{18}$,$\frac{5}{13}$,$\frac{8}{21}$,$\frac{3}{8}$,$\frac{7}{19}$,$\frac{4}{11}$,$\frac{5}{14}$,$\frac{1}{3}$
上の図より、右から7番目の分数は$\frac{5}{13}$ であることがわかります。
(2) (1)であげたポイントの、
操作後の分数の個数 = 操作前の分数の個数 × 2 - 1
を利用していきます。操作5回以降を考えると、
操作5回で17×2-1=33個
→ 操作6回で33×2-1=65個
→ 操作7回で65×2-1=129個
となり、操作7回で並んでいる分数の個数は129個です。
(3) まずは分母の和を「操作4回目」まで表で示してみます。
はじめ → 2+3=5×1
操作1回目 → 2+5+3=10=5×2
操作2回目 → 2+7+5+8+3=25=5×5
操作3回目 → 2+9+7+12+5+13+8+11+3=70=5×14
操作4回目 → 2+11+9+16+7+19+12+17+5+18+13+21+8+19+11+14+3 =205=5×41
・・・・・・・・
少し難しいですが、分母の和を5で割ったもの(1、2、5、14、41、・・・)を(2)のような規則にあてはめて考えます。
2=1×3-1、5=2×3-1、14=5×3-1、41=14×3-1・・・
のように、「3倍して1を引く」ことで、次の数を得ることができます。
よって、操作を5回目以降も続けると、
操作5回目 → 41×3-1=122
操作6回目 → 122×3-1=365
操作7回目 → 365×3-1=1094
操作8回目 → 1094×3-1=3281
となることから、操作8回目でえられる分母の和は、
5×3281=16405になります。
<別解>
これも少し難しい解き方になりますが、1、2、5、14、41、・・・の数列において、隣り合う2数の差(階差)を数列にすると、
1(=2-1)、3(=5-2)、9(=14-5)、27(=41-14)、・・・
という規則があることがわかります。
つまり41=1+(1+3+9+27)となります。
よって、
A=1+3+9+27とすると、その3倍(A×3)は、3+9+27+27×3と表すことができます。
A×3= 3+9+27+27×3
A =1+3+9+27 (-
A×(3-1)=27×3-1=3×3×3×3-1
(↑3を4個かける)
以上より、A=(3×3×3×3-1)÷(3-1)=80÷2=40から、40+1=41をえます。
つまり、操作8回目は、(3×3×3×3×3×3×3×3-1)÷(3-1)+1=3281となり、
(↑3を8個かける)
5×3281=16405を得られることがわかります。
今回の「注目の設問」③のテーマは、ズバリ高校数学で学ぶ「漸化式」を低学年におろして考えさせる問題であったことがわかります。 数論系は、約数倍数をベースにかなり高度なテーマまで扱うのが常態化していますので、規則性の基礎である、「周期算」「等差数列」「植木算」「方陣算」をベースに、「三角数(1から連続する整数の和)」「四角数(平方数)→(1から連続する奇数の和)」など様々なテーマの数列に慣れておく必要があります。 また、この問題が出題されたH27①は、算数の平均点が40点を下回る難問の集まりであり、この問題が「大問5」であることから、取り組みが試験時間終盤になることを余儀なくされることから、 「(1)の分数を探す問題が面倒である」ということで回避し、 (2)を「最短時間でササっと答えを出そう」 と考えてしまいがちです。 分数の個数が「2→3→5→・・・」となっていることから、とっさに「フィボナッチ数列(前2つの数の和)」であると勘違いし、2→3→5→8→13→21→34→55で55個と答えてしまった受験生もいたのではないでしょうか(操作3回目の結果を示さないという罠が仕掛けられています)。 結局「注目の設問」③(「H27①」)は、 (2)だけを細心の注意を払って取り組み正解させれば十分であり、((1)(3)は合否に影響なし)ということができます。 このように市川中学をはじめ難関中学の算数では、「受験生の思い込み(序盤易問で終盤難問、文中での種々の勘違い)」に対し、巧妙に仕組まれた問題配置がよく見られます。 今回はその極端な例をご紹介しましたが、これを克服する方法は、「早期から過去問に取り組む」こと以外にはないと言えます。 市川中学の受験生は2月以降の東京、神奈川校を併願していることが多いですが、市川中学を偏差値だけで判断して受験すると痛い目に遭うことも少なくありませんので、注意が必要です。
Contact Us
会社連絡先
住所
■ 本社オフィス
▶東京都中央区日本橋本石町2‐1‐1
アスパ日本橋オフィス
受付時間:
10:00-22:00
電話:
03-5389-3995
E-mail:
info@alpha-nexus.jp
お問合せフォーム
下記フォームに必要事項を入力後、確認ボタンを押してください。
