家庭教師が教える中学受験の算数
【開智中学編】

具体的な開智中学対策例

【注目の設問①　 H26　2】

みかん3個となし2個は同じ値段で、なし3個の値段は、みかん2個とりんご2個の合計4個の値段と同じです。みかん1個とりんご1個となし1個の合計3個の値段は180円です。
太郎君は、みかん、りんご、なしの3種類の果物をそれぞれ何個か買い、合計で372円払いました。ただし、どの種類の果物も1つ以上は買ったものとします。
(1) みかんの値段とりんごの値段となしの値段の比は何対何対何ですか。
(2) 太郎君が購入した3種類の果物の買い方は、全部で3通りあります。この3通りをすべて答えなさい。例えば、みかんを3個、りんごを7個、なし5個買った場合には、(みかんの個数、りんごの個数、なしの個数)＝(3、7、5)と答えなさい。

【解答解説】

＜以下、みかんの値段＝○み、りんごの値段＝○り、なしの値段＝○な、とします＞
(1)　○み×3＝○な×2より、○み：○な(値段)＝2：3となります。
ここで、○み＝②、○な＝③とすると、
○な×3＝○み×2＋○り×2より、③×3＝②×2＋○り×2、○り×2＝⑨－④＝⑤、
○り＝5÷2＝ 2.5 となります。よって、みかんの値段とりんごの値段となしの値段の比は、2：2.5：3＝4：5：6です。
(2) 3種類の果物をそれぞれ1個ずつ合計3個買うときの値段が180円ですから、
○み＝180÷(4＋5＋6)×4＝48円、○り＝180÷(4＋5＋6)×5＝60円、○な＝180÷(4＋5＋6)×6＝72円とわかります。
ここで、みかんの個数をM、りんごの個数をR、なしの個数をNとすると、
　　　48×M＋60×R＋72×N＝372
という関係式が成立します。さらに48、60、72、372の最大公約数12で割ると、
　　　4×M＋5×R＋6×N＝31
2×(2×M＋3×N)＝31－5×R (⇦ M、Nは最低1ですから2×(2＋3)＝10以上)
上の関係式より、Rは1か3に決まります。

<1> R＝1のとき
2×M＋3×N＝(31－5×1)÷2＝13　→　M＝(13－3×N)÷2
(M、N)＝(5、1)、(2、3)
<2> R＝3のとき
2×M＋3×N＝(31－5×3)÷2＝8　→　M＝(8－3×N)÷2
(M、N)＝(1、2)
以上より求める場合は、(1、3、2)、(2、1、3)、(5、1、1)の3通りです。
このように、「不定方程式」とよばれる(鶴亀と場合の数が融合する)特殊分野が存在し、とらえかたは、大学受験に出る「整数解の方程式」と大差ありませんので、大手進学塾のテキストや参考書、問題集で十分に訓練しておく必要があります。

【注目の設問② H29 2】

太郎君と花子さんの2人が同時に出発して、太郎君は車でA町→B町→A町→B町と(途中休まず一定の速さで)移動し、花子さんは自転車でA町→B町と(一定の速さで)移動します。花子さんは、太郎君の車と初めてすれ違ってから56分後に太郎君の車に追い越され、さらにその84分後に再び太郎君の車とすれ違いました。
その後太郎君は予定を変更して、B町まであと21kmの地点で引き返してA町に向かいました。すると花子さんと同時にA町に到着することができました。

(1) 初めに2人がすれ違ったのは、出発してから何分後ですか。
(2) 太郎君と花子さんの速さの比は何対何ですか。
(3) A町からB町までの道のりは何kmですか。

【解答解説】

式と計算で解こうにも数量が「56分」「84分」「21km」の3つしか出てきませんので、まずは「56分」「84分」の部分が表されるグラフに示してみます。

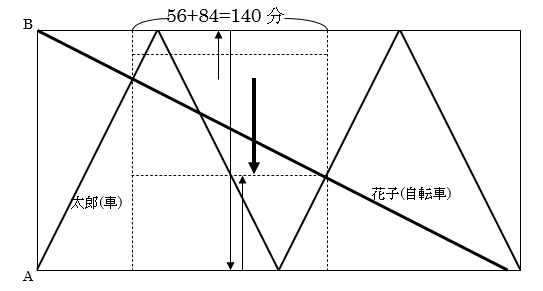
(1)　かなり大雑把ですが上のグラフで、太郎君と花子さんが初めてすれ違ってから2回目にすれ違うまでに56＋84＝140分かかってます。
このとき、2人が進んでいる道のりの和は、AB間の道のりの2倍にあたります。2人が同時に出発してから初めてすれ違うまでに、進んだ道のりの和はAB間の道のりにあたりますので、2人が初めてすれ違ったのは、2人が出発してから、140÷2＝70分後だとわかります。

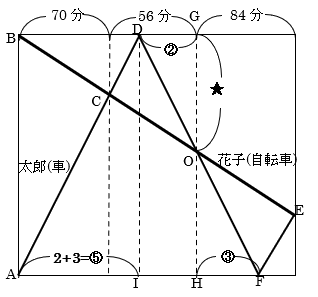
2つの三角形OCD、OEFの相似比が、
OC：OE＝56：84＝2：3
となるので、
OD：OF＝2：3、DG：FH＝2：3
となります。
ここで、DG＝IH＝②、HF＝③とすると、AI＝2+3＝⑤となります。
グラフの「★」の部分の道のりを進むのにかかる時間は、
太郎：花子(時間)＝②：(②＋⑤)＝2：7より、
速さの比は逆比の7：2となります。

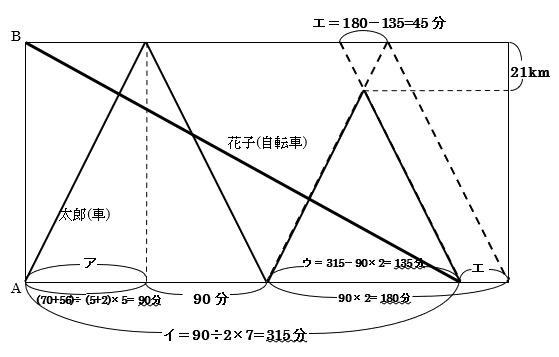
(3)　問題文の最後の2行にある様子を示したものが下のグラフです。
ひとつひとつ条件を整理していくと、まず太郎君の車がAB間片道を進むのにかかる時間(ア)は、(2)のグラフを利用して、(70+56)÷(5+2)×5＝90分、
花子さんがB町からA町へ進むのにかかる時間(イ)は、(2)の結果を利用して、
90÷2×7＝315分、
太郎君が2回目にA町を出発してから、B町の21km手前で折り返して再びA町に戻ってくるまでの時間(ウ)は、
315－90×2＝135分、
太郎君が往復する時間の、「1回目と2回目の差(エ)」は、
180－135＝45分
とわかります。
下のグラフにできる相似形に注目して、21：AB＝45：180＝1：4
とわかりますので、AB間の道のりは、21÷1×4＝84kmです。

※このような「情報が掴みにくい旅人算」は、大雑把にグラフに落とし込んでみると、全貌が明らかになることが多いです。
よって、(やや難解な文章のみの)旅人算をグラフに落とし込む訓練も是非しておいて下さい。グラフは(時刻、位置)が的確に表せるので有効な解法手段であると言えます。


【注目の設問③ H27 5　】

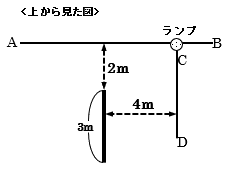
平らでとても広い床の上に直線ABがあります。直線AB上の点Cの真上の高さ8mのところにランプがあります。同じ床の上にある直線CDは、直線ABに対して垂直です。ただし、ランプの大きさは考えません。
(1) たて3m、高さ4mで光を通さず、厚さを無視できる薄い板があります。図のように、直線CDと平行で、CDから4m、直線ABから2m離れたところに、床に対して垂直になるよう板を立てます。このとき、床にできる影の面積は何m2ですか。

　

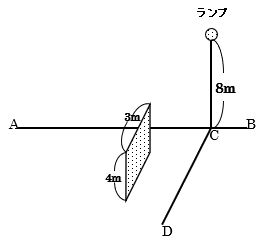
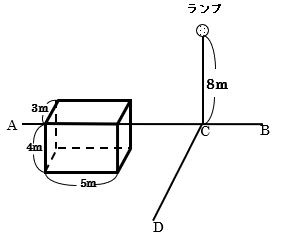
(2) たて3m、横5m、高さ4mで光を通さない直方体があります。直線ABから直方体は2m離れた状態を保ちながら、直線ABの向きにそって動かします。直線CDと直方体の間の長さをアとします。
(a) アが4mのとき、床にできる直方体の影の面積は何m2ですか。

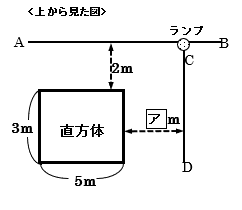
(b) 影の面積が90m2となるとき、 アは何mですか。

【解答解説】

※最近共学の難関校でよく出題される「立体の影」です。「立体切断」と同様に、3方 向からとらえますが、相似比のわかる方向から順に量の関係をとらえます。この問題で は、まず「真正面」(CとDが一致する方向)からとらえます。

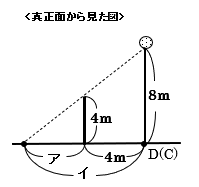
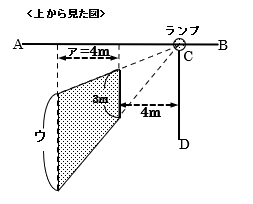
(1) 上の左の図は、見取り図を真正面から見たものです。相似な2つの直角三角形に注 目すると、ア：イ＝4：8＝1：2となり、ア＝4÷(2－1)×1＝4mとわかります。
それを踏まえ、右の図は問題でも示された「上から見た図」で、ア＝4mと分かったことで、板によってできる影が、右の網目部分のような台形で表されます。
台形に関わる2つの三角形の相似に注目すると、
3：ウ＝4：(4+4)＝1：2より、ウ＝3÷1×2＝6mと分かりますので、求める面積は、
(3+6)×4÷2＝18m2です。
(2) (1)と同様に考えると、ランプによる直方体の影は、下の図のようになります。
高さの比が(1)と同じで4：8＝1：2となりますから、これを踏まえ、真上から見た図で細かい量を表していきます。

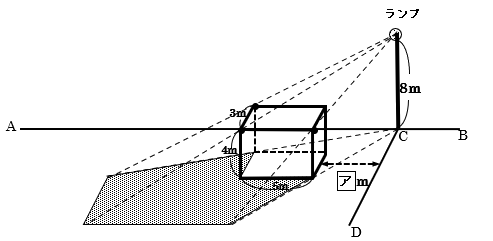
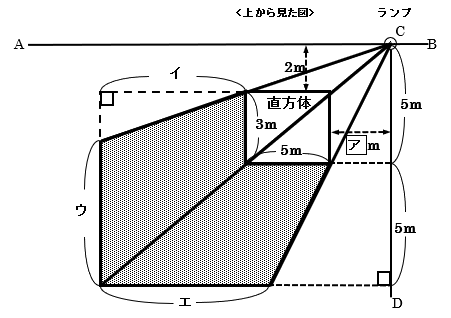
上の図で、「相似比1：2」を利用すると、イ＝ア＋5m、ウ＝3÷1×2＝6m、 エ＝5÷1×2＝10mとなります。
網目部分の面積が90m2ですから、
　(3＋6)×(ア＋5)÷2＋(5＋10)×5÷2＝90
の関係式が成り立ちます。
よって、
　ア＝(90×2－75)÷9－5＝105/9－5＝(35-15)/3＝62/3cm2
となります。
※共学の難関校では、「立体切断」やこの「立体の影」がよく出題されており、この10年程を見ても、出題する学校は増加傾向にあります。従ってこの2つは絶対に外せませんので、「見取り図」、「投影図」から相似を正確にとらえる訓練が必要になります。

【まとめ】

最近の傾向として、開智では「先端」、「一般第1回」の試験問題の難度差が以前より小さくなってきています。ただ「スライド制度」などから、やはり合格する受験生のレベルは分けているようですが、いずれのコースを選ぶにせよ、過去問対策は遅くとも夏前には始める必要があります。
また「60分」という時間は余裕があるようで実際はあっという間に過ぎてしまいますので、この意味でも「過去問対策」は1日も早く開始すべきです。
今回は扱いませんでしたが、「数論系（数の性質・規則性・場合の数）」にも十分に時間を費やし、「標準から発展」までしっかり演習を積んでおく必要がありますので、頑張っていただきたいと思います。

Contact Us