
家庭教師が教える中学受験の算数
【桜蔭中学編】
留意点1
桜蔭中の算数入試問題は6割(明らかに問題が易しければ7割)を目標に!
試験時間50分で大問は4題。設問数は15題前後であるものの全体的に数値の取り扱いが厄介です。また、出だしの計算問題からボリュームがあるため、毎日の計算練習は欠かせません。
強化すべき単元は、規則性、点の移動、立体図形などですが全て高難度な問題です。
留意点2
受験学年の前にすべての単元について習得を済ませて応用力を鍛える必要があります。
なるべく早い時期から過去問演習を繰り返し、手を付ける順番を考えながら問題を解くスピードを上げる訓練をしなければなりません。
「解答用紙」は大問Ⅱ以降がすべて考え方をみる問題になっています。
留意点3
桜蔭中学の算数問題は記入欄が非常に狭いため、記入欄には求め方を要約してから記入する必要があります。これを本番で実行出来るよう過去問を解く際に訓練しておかねばなりません。
また、毎年出題されているのが「規則性」です。規則性単体の問題も多いものの、難度の高い他の単元との融合問題も多いので十分な反復演習が必要になります。
具体的な桜蔭中学対策例
【注目の設問① H27 1】
図1のようなアからケの9個のマスがあります。 このアからケのマスの中に、約数が全部で9個ある 整数を小さい順に入れます。例えば、36の場合は図2
ようになります。このとき、次の□にあてはまる数を 答えなさい。
① アとケとオに書かれている数字の和が241 となる整数は□です。
② ウとケとキに書かれている数字の積が38416 となる整数は□です。

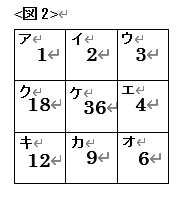
図2で配置された「36の約数」のうち、エからケに配置された数を、ずべて素因数分解(素数に分解)してみます。
| $1$ | $2$ | $3$ |
| $2 \times 3 \times 3 $ | $ 2 \times 2 \times 3 \times 3$ | $ 2 \times 2 $ |
| $2 \times 2 \times 3 $ | $3 \times 3 $ | $ 2 \times 3$ |
表のように、「約数が9個ある整数」は、2種類の素数$A、B$ $(A < B)$にて、 $ A \times A \times B \times
B$ (2種類の素数$A、B$の2個ずつの積)の形で表せます。
① ア$=1$、ケ$=A \times A \times B \times B$、オ$=A \times B$
と表されるので、
ア+ケ+オ$ =1+A \times A \times B \times B + A \times B = 241 $
より、
$ A \times A \times B \times B + A \times B $
$ = A \times B \times (A \times B + 1)= 241 - 1 = 240 $
$ = 15 \times 16 = 15 \times ( 15 + 1) $
$ = 3\times 5 \times ( 3 \times 5 + 1 )$
となりますから、求める整数ケは、$3 \times 3 \times 5 \times 5 =225$です。
※①だけを考えるのであれば、$ A \times B =X$ として、ア+ケ+オ$ =1 +X \times X +X =241$、 $ X
\times (X +1)$$=240$$=15 \times 16 $$=15 \times (15 +1) $より、ケは$ 15 \times 15
=225$です。
② ウ=$B$、ケ$= A \times A \times B \times B$、キ$= A \times A \times B$と表されるので、
ウ×ケ×キ$= B \times (A \times A \times B \times B) \times (A \times A \times
B) $
$= (A \times A \times B \times B) \times (A \times A \times B \times
B) $
$ = 38416 $$=(2 \times 2 \times 7 \times 7 )$$ \times (2 \times 2 \times 7
\times 7 )$ となりますから、求める整数ケは、$ 2 \times 2 \times 7 \times 7 =196$です。
この問題は、サンプルで「36」の表が出ていましたが、現実には「約数の個数が~個ある整数」の素因数分解による構造にピンとくれば、サンプルがなくても最短距離で正解を導き出すことができます。
約数の個数が1個は「1」のみ、約数の個数が2個は素数、 約数の個数が3個 → 同じ素数2個の積、 約数の個数が4個 → 同じ素数3個の積、あるいは、異なる素数2個の積
このくらいは覚えておく必要があります。
【注目の設問② H29 2】
図は、$AD =DH =16cm$、$GH =12cm$の直方体 $ABCD-EFGH$で、$AF=20cm$です。2つの動く点$P$と $Q$が同時に出発して、毎秒$2cm$の速さで、点$P$は長方形
$ADGF$の周上を、点$Q$は三角形$CDG$の周上を次のように 動きます。
点P:A→D→G→F→A→D→G→・・・ 点Q:G→D→C→G→D→C→・・・
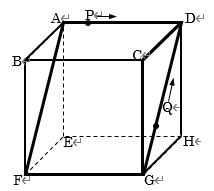
(1) 2点$P、Q$が初めて出会うのは、2点が出発してから何秒後ですか。
(2) 2点$P、Q$が4回目に出会うのは、2点が出発してから何分何秒後ですか。
【解答解説】
ご覧の通り「点の移動」でこの学校でも よく出題されますが、 ・動く点が2つ(以上) ・動く点の通る辺に異なる部分がある というだけで、「出会うまでの時間や出会う場所」 を求めることが、かなり困難になります。 動く点の速さがどちらも「毎秒2cm」という のが、やや救いであるといったところです。 点P:A→D→G→F→A→D→G→・・・ 点Q:G→D→C→G→D→C→・・・
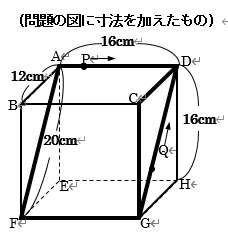
整理① まず、点$P、Q$がそれぞれ「A→D→G→F→A」「G→D→C→G」のように1周する間の、各頂点の所要時間を求めます。 点P:A→D(16÷2=8秒後)→G(8+20÷2=18秒後)→F(18+8=26秒後)→A(26+10=36秒後) 点Q:G→D(20÷2=10秒後)→C(10+12÷2=16秒後)→G(16+8=24秒後) (1) 点$P、Q$が初めて出会うのは、2点が同時に辺DG上にいるときで、①より、点PがDに到着する8秒後から、点QがDに到着する10秒後までの間にあることがわかります。
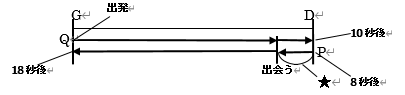
点$P、Q$は速さが同じ(2cm/秒)で、上の図の★は点$P、Q$とも同じ時間がかかるので、求める時間は、$8+(10-8)\div2=(8+10)\div2=9$秒後です。 整理② 整理①を踏まえ、点P、Qが2回目以降に辺DG上を通過する時間を示しておきます。 点P:44~54秒後、80~90秒後、116~126秒後、152~162秒後、・・・ 点Q:24~34秒後、48~58秒後、72~82秒後、96~106秒後、120~130秒後、・・・ < 2回目、 3回目、 4回目>
(2) 整理②より、点P、Qが4回目に出会うのは、120秒後から126秒後までの間であることがわかります。(1)と同様に考えると、出会うのは(120+126)÷2=123秒後より、 2分3秒後であることがわかります。
このように、桜蔭では「地道に調べ上げ活路を見出す問題」が特に「複雑な規則性」にからむ問題として出題されますので、入試時はそのような問題に立ち向かう覚悟が必要です。よって、過去問や「条件整理の面倒な問題」に数多く触れておくことです。上の整理①②を通じ、最終解答を求めるところでは、答えが分数である場合にも備えて線分図やグラフを利用して緻密な解法を心がけてほしいです。
【注目の設問③ H30 1 (1)】
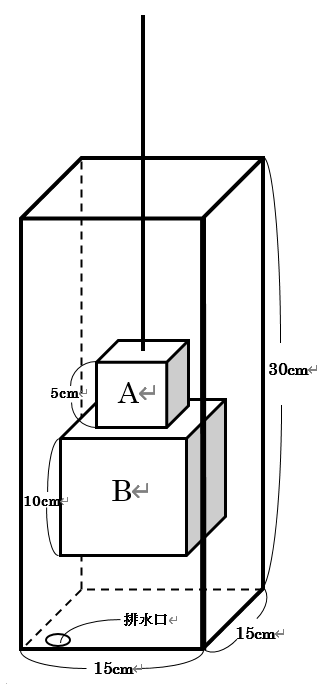
図のように、立方体A、Bをはなれないようにくっつけて重りを作り、直方体の透明な水そうの中にひもでつるします。
重りの下の面は水そうの底面から$ 5cm $のところにあり、常に水そうの底面と平行です。 水そうの中は、最初水で満たされていて、底面の排水口から毎秒$50cm^3$
の割合で排水します。
また、排水を始めると同時に、重りをつるしたひもを毎秒$ \frac{1}{2}cm$ の速さで上にひき上げます。 ただし、水の浮力やひもの体積、水そうの厚みは考えないものとします。
(1) 水面の高さがAの上の面より$1cm$上になるのは、排水を始めてから何秒後ですか。
(2) 水面の高さがAの上の面より$1cm$上になったとき、今度はひもを毎秒$\frac{1}{2}cm$の速さで下ろすことにします。 排水は変わらずに続け、重りは排水口をふさぎません。
重りが水そうの底面に着地した後は、ひもを動かさず、排水だけ続けます。
① 重りが水そうに着地したとき、水面は水そうの底面から何$cm$のところにありますか。
② 排水を始めてから$75$秒後、残っている水の体積は何$cm^3$ですか。このとき、水面は水そうの底面から何$cm$のところにありますか。
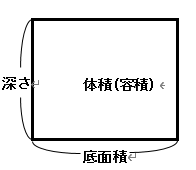
「面積図」を使って、複雑な条件を整理します。
(1) 図1のように、考える装置を「面積図」で表しています。
まず、満たされている水を、毎秒$ 50cm^3$で排水するとき、毎秒$\triangle{cm}$ ずつ水面が下がるとすると、水そうの底面積$
15cm \times 15cm = 225cm^2$ に$\triangle{cm}/秒$をかけると$50cm^3/秒$となるので、$\triangle{}=50
\div 225= \frac{2}{9}cm/秒$とわかります。
図のように、重りAの上の面は、はじめ水面より$10cm$下にあるので、水面が重りAの上の面より$1cm$上になるのは、 $ (10-1) \div
(\frac{2}{9}+ \frac{1}{2}) $ $=9 \div \frac{13}{18} $ $=12 \frac{6}{13} $ 秒後とわかります。
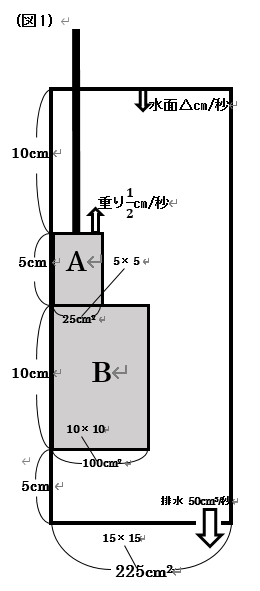
(2) ① (1)のあと、図2のように、重りの下の面は水そうの底面から、 $ 5+\frac{1}{2} \times 12 \frac{6}{13} $ $ = \frac{65+81}{13}= \frac{146}{13}cm (ア) $ のところにあります。 このあと、重りは$\frac{1}{2}cm/秒$で下に下ろしていきます。 右の図の状態から、重りの下の面が、水そうの底面に着地するまでに、 \[ \frac{146}{13} \div \frac{1}{2} = \frac{292}{13}秒\] かかります。 この時間に、水面は \[ \frac{2}{9} \times \frac{292}{13}= \frac{584}{117}cm(イ)\] 下がったので、重りが水そうの底面に着地したとき、水面は水そうの底面から、 $ 1+15+\frac{146}{13}-\frac{584}{117} $ $=\frac{2692}{117}=22\frac{28}{117}cm(□) $ のところにあります。
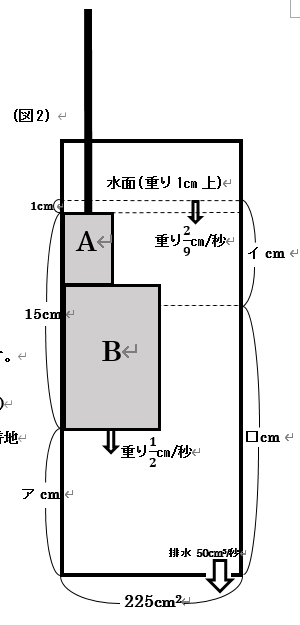
(2) ② 図3のように、初めて重りの下の面が水面の底面に着地するのは、排水を始めてから、$12 \frac{6}{13}+\frac{292}{13} = \frac{454}{13} = 34\frac{12}{13}$秒後です。 よって、排水し始めてから75秒後には、重りの下の面は水そうの底面に着地しています。 重り全体(A+B)の体積は、$5 \times 5 \times 5$$+10 \times 10 \times 10 $$= 1125cm^3 $ですから、はじめに水そうに入っていた水の体積は、$225 \times 30 - 1125 = 5625cm^3 $です。 よって、排水を始めて75秒後に、水そうに残っている水の体積は、$5625 - 50 \times 75 = 1875cm^3$です。 このとき、重りのBの高さまでに入った水の体積は、$(225 -100) \times 10 = 1250cm^3$、重りのAの高さ($5cm$)分の容積は$ (225-25) \times 5=1000 cm^3 $ ありますから、 \[ 1875-1250 =625>1000 \] より、水面は重りのAの部分にあることがわかります。 よって、求める水面の高さ(□)は、 $ 10+625 \div (225 - 25) $$= 10 + \frac{625}{200} $$ =13\frac{1}{8}cm $ であるとわかります。

既に気づかれた方も多いと思いますが、この問題に関しては、最後の(2)②が一番取っ掛かり易いということがわかると思います。一般に、図形や点の移動の問題で、動かす図形の速さがわかっている場合は、
「〇秒後(今回は75秒後)」がはっきりしている問題から手を付けるのがセオリーです。
最高レベルの中学受験の問題になると、そういった「思い込みの強い受験生」をふるい落とす罠も仕掛けてありますので、実戦をたくさん積んで対応力を身に着けておくことが重要です。
私立中学女子校の最難関である桜蔭中学対策編、如何でしたでしょうか。高度な知識を自在にこなすテクニックが要求されることがお判りいただけたかと思います。
一般に、男子に比べ女子の方が精神的な成長が早いことを見越してか、特に女子難関校では男子難関校に比べ、問題用紙や解答用紙のスペースが狭くなっていますから、早めに過去問の現物コピーを利用した実戦訓練を積み上げ、トライアル・アンド・エラーを繰り返して対処するしか方法がありません。
数論系(数の性質・規則性・場合の数)における高度な知識、高度な図形問題の解法力、図・表・グラフの積極的な活用など、問題をこなすにあたっては「量より質」を重んじ、中学受験で志望校合格を勝ち取っていただきたいと思います。
Contact Us
会社連絡先
住所
■ 本社オフィス
▶東京都中央区日本橋本石町2‐1‐1
アスパ日本橋オフィス
受付時間:
10:00-22:00
電話:
03-5389-3995
E-mail:
info@alpha-nexus.jp
お問合せフォーム
下記フォームに必要事項を入力後、確認ボタンを押してください。
