
家庭教師が教える中学受験の算数
【豊島岡女子学園中学編】
留意点1
豊島岡女子中学の算数の試験時間は50分で解答のみを書き入れる形式になっています。 大問は6題、設問数は18題で概ね一定しており、一般的には「大問1、2の計算・独立問題8題で全問正解必須」と言われています。 もちろんこの8題を確実に取ることが肝要ですが、実はこの中に数問の難問が潜んでいることがあるので、それらに無理に拘ることなく「一旦後回し」にする戦術で攻めることも考えなければなりません。
留意点2
女子校の中では図形の難易度が最高レベルにあるため(平面・立体ともに超難関男子中学レベル)、「緻密な作業の繰り返し」や「見抜きにくい特徴の解明」などの高度なテクニックが必要になります。 そこで豊島岡女子中学の過去問対策の他に、受験する他校の中で特に「難関共学校」や「難関男子中学」の図形問題がよい練習台になるため、それらの問題を活用することも有効な対策になります。
留意点3
目標点としては、第1回と第3回が6割5分、第2回は6割を目標にしてください。 まずは6年生のなるべく早い時期(遅くとも夏休み前)から、過去問を中心とした実戦演習を開始し、特に「問題用紙の効果的な活用」を意識して訓練していく必要があります。 また漫然と初めから解いていくのではなく、「解く順番」についても毎回検証することが、無駄に考える時間的なロスを最小限に抑える訓練となります。
具体的な豊島岡女子学園中学対策例
【注目の設問① H24 2-2】
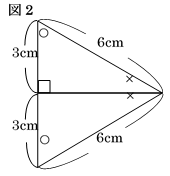
図のように、点$O$を中心とする円の一部 があり、$\angle AOB$は直角です。円周の上に点$C$を とり、半径$CO、BO$の上にそれぞれ点$P、Q$を とります。 このとき、点$P$は半径$CO$の真ん中の点で、 $\angle APO$と$\angle CQO$も直角になりました。 図の色のついた(ア)の部分の面積と、図の色の ついた(イ)の部分の面積の差は何$cm^2$ですか。 〔円周率:3.14〕
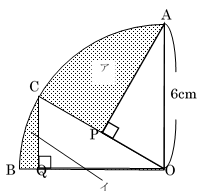
図1で、$OC$は円の一部(おうぎ形)の半径につき、
$OA$に等しく$6cm$です。次に三角形$AOP$と三角形
$OCQ$は、「1辺の長さ($6cm$)とその両端の角の大きさ
(〇と×)」がそれぞれ等しく合同になります。
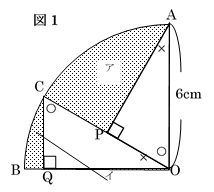
さらに、$OP$の長さが$OC$の長さの半分で、$6 \div 2=
3cm$となり、三角形$AOP$と三角形$OCQ$を図2
のように組み合わせると、1辺の長さが$6cm$の正三角
形になるので、
〇$=60°$、×$=60 \div 2 =30°$
であるとわかります。
よって、アの部分とイの部分の面積の差は、三角形
$AOP$と三角形$OCQ$が合同であることから、
おうぎ形$OAC$とおうぎ形$OCB$の面積の差となり、
$6 \times 6 \times 3.14 \times \frac{60}{360}-6 \times 6 \times 3.14 \times \frac{30}{360}$
$=3.14 \times 36 \times \frac{1}{12}=9.42 cm^2$です。
この問題は「絶対に落とせない問題」ということになりますが、大問2の3問目とい う計算・独立問題の後半ということで、注意力の低下で「何を求めるのかを勘違い」してしまい、無駄な時間を費やしてしまうケースも多くなりますので、もしもそうなってし まったときは、迷わず「一旦後回し」にすべきです。大問3以降を先に解いてきてから、 問題を読み直す方が、冷静にしかも正確に解けるものです。
【注目の設問② H29 4】
中心が同じ点である2つの円があり、大きい円 は1周$18cm$、小さい円は1周$9cm$です。点$P$は 大きい円の周の上を時計回りに毎秒$3cm$の速さで 動き、点$Q$は小さい円の周の上を時計回りに毎秒 $2cm$の速さで動きます。最初、右の図のように、 点$P$、点$Q$と円の中心$O$が、この順に一つの直線 の上にあり、点$P$と点$Q$は同時に動き始めます。 このとき、次の各問いに答えなさい。
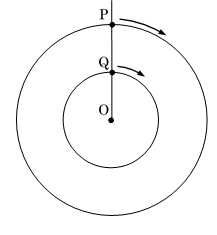
(1) 点$P$、点$Q$が動き始めてから、3点$O、P、Q$が初めて一つの直線の上に並ぶのは何秒後ですか。
(2) 3点$O、P、Q$を結んでできる三角形が初めて直角三角形になってから、次に直角三角形になるまでに何秒かかりますか。
(3) 点$P$、点$Q$が動き始めてから、180秒後までに間に、3点$O、P、Q$を結んでできる三角形が直角三角形になるのは全部で何回ありますか。
まず、$P、Q$の速さを、角速度(度/秒)に変換します。
<1周にかかる時間>
$P:18÷3=6$秒 、$Q:9÷2=4.5$秒
<1秒間に動く角度(角速度)>
$P:360÷6=60$度/秒 、$Q:360÷4.5=80$度/秒
(1)
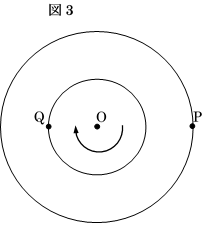
$P、Q$が初めて図3のような位置に
なったとき(動く角度の差が180度になったとき)
ですから、$180 \div (80-60)=9$秒後です。
(2)
大きい円と小さい円はどちらも中心が$O$で、周の長さの比が$18:9=2:1$ですから、
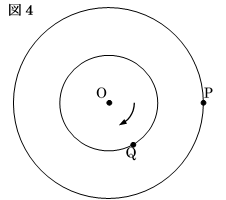
半径の比も$2:1$となります。図4より、$\angle OQP$が直角になるとき、$OQ$の延長上
と大きな円との交点を$R$とすると、$OR$は$OQ$の2倍、三角形$OPQ$と三角形$RPQ$
が合同、三角形$OPR$が正三角形になるので、$\angle POQ$の大きさが60度になります。
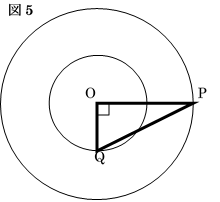
そこから、図5のように$\angle POQ$が直角になるまでの時間を求めればよいので、
$(90-60) \div (80-60)=1.5$秒後です。
(3)
(2)より、三角形$OPQ$が直角三角形になるのは、$\angle POQ$の大きさが60度のときと90度のときの2通りあることがわかりますから、$\angle POQ$の大きさの変化をグラフに表してみます。(1)で$\angle POQ$の大きさが180度(一直線)になるまでに9秒かかることから、下のグラフ1のようになります。
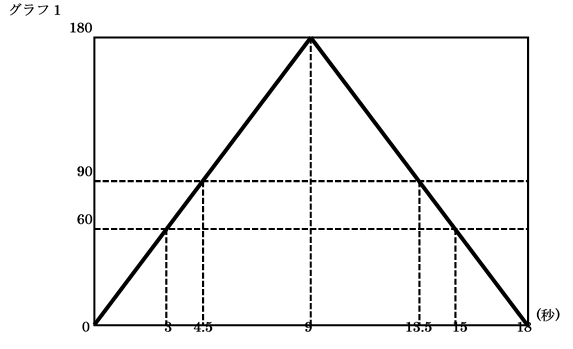
このように、点$P、Q$が出発してから、$\angle POQ$が再び0度になるまでには9×2=18
秒かかり、この間に三角形$OPQ$が直角三角形になるのは、3秒後、4.5秒後、13.5秒
後、15秒後の4回あります。よって、180秒の間に三角形$OPQ$が直角三角形になるの
は、$4 \times (180 \div 18)=40$回あります。
※はじめの条件で、「円周の長さと動点$P、Q$の速さ」が与えられましたが、この設定
で設問に解答するのはかなり困難ですから、「角速度に変換する」のが、最も一般的な解法です。つまり「時計算」のように考えればよいわけです。このように「動く図形」はほぼ毎年出題されていますので、作図、表・グラフの作成は訓練しておくべきです。
【注目の設問③ H26 6】
図6のように、1辺の長さが$4cm$の 立方体$ABCD-EFG$Hがあります。 正方形$ABCD$の対角線が交わる点を$I$とし、 点$I、E、F、G、H$を頂点とする立体$S$を考え ます。このとき、次の問いに答えなさい。
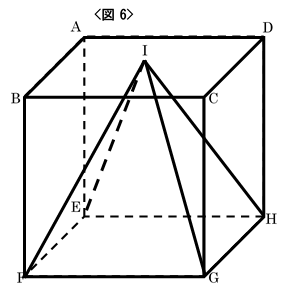
(1) 図7のように、点$E$と点$C$を結んだ 直線$EC$と立体$S$の辺$IG$が交わる点を$J$とします。 $EJ:JC$を求めなさい。
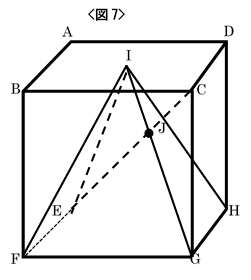
(2) 図8のように、辺$AB$上に$AL:LB=2:1$となる点$L$、辺$EF$上に$EM:MF=2;1$となる点$M$、辺$HG$上に$HN:NG=2;1$となる点$N$をそれぞれとります。
3点$L、M、N$を通る平面で立体Sを切り
ます。
① 切り口の平面と立体$S$の辺$IG$が交わる点を$P$とします。
$IP:PG$を求めなさい。
② 切り口の面積は何$cm^2$ですか。
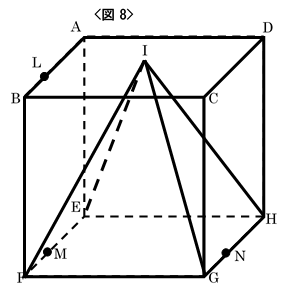
(1)
投影図に表すと、相似形が表れて辺の比が明らかになります。問題の条件と図9
より、$I$が$AC$の真ん中にあるので、図10より、三角形$JCI$と三角形$JEG$の相似の
関係から、$EJ:JC=EG:CI=2:1$であるとわかります。
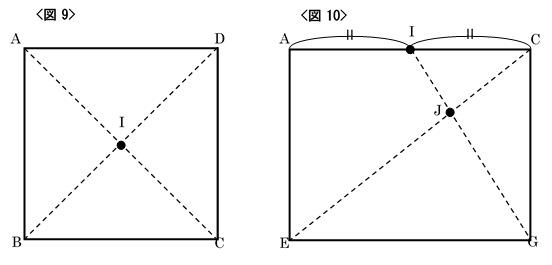
(2)
問題文より、まず見取り図で3点$L、M、N$を通る平面で立体$S$を切断する様子を表
したものが図11です。このときの細かい数量関係を表すため、(1)と同様に投影図で考え
ます。(切断する平面と$IF$の交点を$Q$とします。)
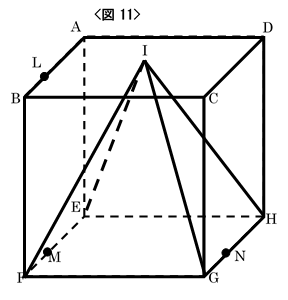
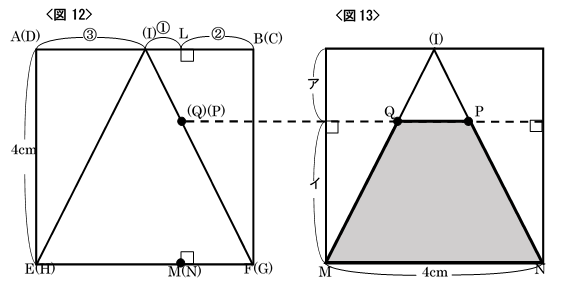
3点$L、M、N$で切る平面を、$M$と$N$が一致する方向からみて直線$LM$で表したものが図12です。また左の図を受けて切り口を表したのが図13です。 ① 図12より、各部分の相似を考慮して$IP:PG=1:2$です。 ② (1)の結果と図12より、ア:イ$=LQ:QM=IP:PG=1:2$となるので、図13で イ$=4 \times \frac{2}{1+2}=8/3cm、QP:MN=1:(1+2)=1:3$より、$QP=4 \times \frac{1}{3}=\frac{4}{3}cm$です。 よって、切り口(台形$QMNP$)の面積は、$(\frac{4}{3}+4) \times \frac{8}{3} \times \frac{1}{2}=7\frac{1}{9} cm^2$です。
※豊島岡女子中学では「立体切断」分野の対策が不可欠となります。今回扱った問題レベルであれば、豊島岡女子中学の算数の入試問題全体を考えると、全問正解を目指す必要があります。 辺の長さ、あるいは辺の比がわかる面からとらえていき、できるだけ細かくていねいに図で表すことが大切です。
【まとめ】このように豊島岡女子中学の算数では、「図形」対策が如何に重要であるかがおわかりいただけたと思います。ここで示した問題以外にも、「図形の移動」や「水量変化」など、難関校で出題される代表的な問題については何を出題されても対応できるという準備をしておく必要があります。 また、問題が難しい割に合格基準が高いことを考慮すれば、「図形全般」に関し、「得意」ではなくても「不得意分野を作らない」という姿勢で日頃から問題に取り組むことが大切です。 最後に扱った「立体切断」は、女子校の中で頻繁に出題するのは豊島岡女子中学を含め数校しかありませんが、併願校に共学の難関校があれば「立体切断」の演習は十分にできますし、無駄になることはありません。 入試は図形以外にも「割合・比」、「数論」、「速さ」、「新傾向思考力」など多岐にわたりますので、どの分野も「標準から発展」のレベルにしっかり手が出せるようなレベルに仕上げておくことが重要です。 豊島岡女子学園中学校合格に向けて、是非とも頑張ってください。
Contact Us
会社連絡先
住所
■ 本社オフィス
▶東京都中央区日本橋本石町2‐1‐1
アスパ日本橋オフィス
受付時間:
10:00-22:00
電話:
03-5389-3995
E-mail:
info@alpha-nexus.jp
お問合せフォーム
下記フォームに必要事項を入力後、確認ボタンを押してください。
