家庭教師が教える中学受験の算数
【早稲田中学編】
留意点1
算数は60点満点中40点を目標に!強化すべき単元は平面図形の角度・面積・長さ・移動
立体図形は体積・表面積・水量変化である。
高難度な図形も得点源にする必要がある。
早稲田中の算数入試問題は、試験時間50分に対し、設問数が15題(毎年ほぼ均一)で
あることから、1問平均3分20秒をかけることができる。
留意点2
しかし、設問数が少ない分、すべての問が標準レベル以上(難問も多数)となっている為、
塾のテキストや参考書・問題集で解き方を覚えただけでは、到底歯が立たない。
よって、なるべく早い時期から過去問演習を繰り返し、「死守すべき問題」と「捨て問題
」をはっきりさせる習慣をつけなければならない。
留意点3
そこで、過去問実施後、その判断が正しかったかどうか検証することが重要である。
また、「解答のみ記入する」出題形式であっても、問題用紙を有効活用し、「途中の考え
方を工夫して記述する姿勢」を身に着けることが重要である。
特に「1問目」は要注意!
具体的な早稲田中学対策例
【注目の設問① H28 第2回 2-(1)】
円周率は3.14とします.
図は、四角形とおうぎ形を重ねた図形です。斜線部分の面積は何$cm^2$
ですか。ただし1辺が$2cm$ の正三角形の面積は$1.73cm^2$とします。
【解答解説】
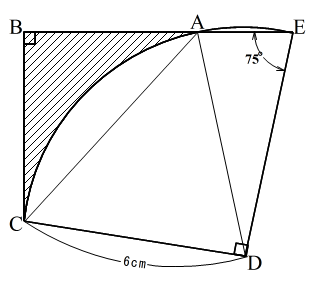
図1
図1のように、おうぎ形の中心DからDA(AはBEと弧CEの交点)、およびACをひきます。DC、DA、DEはすべておうぎ形の半径ですから、長さはすべて6cmです。よって、三角形DAEは二等辺三角形となり、角DAEの大きさは角DEAの大きさに等しく75°となります。さらに、角ADEの大きさは、180-75×2=30より30°となり、角ADCの大きさは、90-30=60より60°となります。よって、 角DACと角DCAの大きさは、(180-60)÷2=60より60°となり、三角形ACDは、1辺6cmの正三角形となります。
一方、角BACの大きさは、180-(75+60)=45より45°となります。
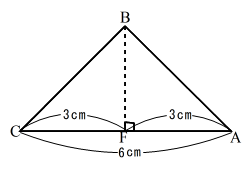
図2
図2のように、三角形ABCは、角ABCの大きさが90°、角BAC、角BCAの大きさが45°となることから直角二等辺三角形であることがわかり、ACを底辺とみたときの高さBFの長さは、6÷2=3より3cmとなります。

図3
図3より、三角形ACDと1辺2cmの正三角形(網目部分)は、相似比が6:2=3:1となり、面積比が3×3:1×1=9:1となりますから、三角形ACDの面積は、1.73×9=15.57より15.57cm2となります。
したがって、求める斜線部分の面積は、
三角形ABCの面積+三角形ACDの面積-おうぎ形ACDの面積
ということになり、
6×3÷2+1.73×9-6×6×3.14×60/360=5.73より5.73cm2となります。
以上のように、この問題は、補助線を引き角度を明らかにすることで、二等辺三角形・正三角形・直角二等辺三角形を発見し、さらには、与えられた条件「1辺2cmの正三角形の面積は1.73cm2」を、相似比と面積比の関係に関連付けて利用し、面積を求めるなど、かなり高度な平面図形の解法能力が必要になってきます。
9月以降の追い込み時期には、毎日1、2題ハイレベルな平面図形に取り組み、十分に鍛えてから受験に臨むことをおすすめいたします。
【注目の設問② H27 第1回 5】
上の図1のような、3辺の長さが20cm、32cm、16cmである直方体の容器の中に、直方体の形をした石Pを入れて、毎分800cm3の割合で水を入れていきました。石の置き方は(斜めに置くことはできません)3通りありますが、うち2通りは10分33秒で水があふれ出し、残りの1通りは11分36秒で水があふれ出しました。
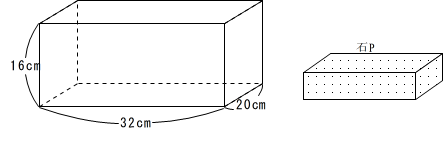
図1
図2は3通りの石の置き方についての時間と水位の関係を1つのグラフに表したものです。
(1)石Pの体積は何cm3ですか。
(2)石Pの最も長い辺の長さは何cmですか。
(3)グラフのaとbの差は5分36秒です。石Pの最も短い辺の長さは何cmですか。
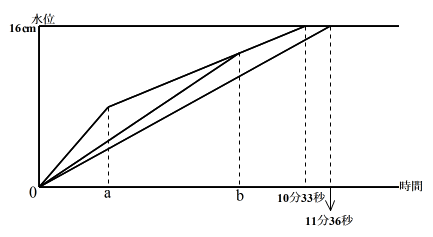
図2
【解答解説】
 図4,5,6
図4,5,6
(1)図4、5の入れ方は、水そうに石Pを完全に沈めているので、
石Pの体積は、「容器の容積-10分33秒入れた水の体積」で求まり、32×20×16-800×1033/60=1800より1800cm3です。
(2) 図6のように石Pを水そうに入れたとき、図7のような石Pの面ウを底面にして水そうに水を入れることになり、11分36秒かかるので、石Pの水そうよりも上に出ている部分の体積は、800×(1136/60-1033/60)=840より840cm3です。

図7
よって図8のように、石Pの最も長い辺(□)の長さと水そうの深さの比が、石Pの体積と石Pが水につかっている部分の体積の比に等しいので、
□:16=1800:(1800-840)=15:8より、石Pの最も長い辺の長さは、16×15/8=30より30cmとなります。
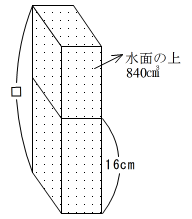
図8
まず、石Pの面ウの面積は、1800÷30=60より60cm2です。
また、図9と条件より、★の部分の容積は、グラフ中の「aとbの差が5分36秒」であることから、800×536/60=4480より4480cm3です。
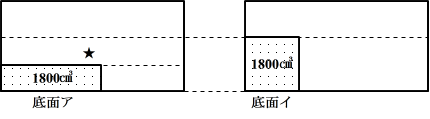
図9
よって、石Pの底面をアとしたときと、底面をイとしたときの高さの差は、石Pの面ウの縦と横の辺の長さの差に等しくなるので、4480÷(32×20)=7より7cmです。積が60、差が7の2つの数は、60の約数を並べてみると、
1、 2、 3、 4、 5、 6、 10、 12、 15、 20、 30、 60
以上から6と12であることがわかり、石Pの最も短い辺の長さは5cmとわかります。
水量変化の問題は、苦手にしている受験生が多く、難関校では数多く出題されており、早稲田で出題される場合、毎回最高水準レベルであるといっても過言ではありません。そのためには、「グラフ」というものにいかに慣れておくかが重要で、出発単元は「速さ」ということになります。「1人の動きのグラフ」「旅人(2人以上)のグラフ」「点の移動」そして「水量変化」という、すべての頻出パターンを応用レベルまで十分に演習し鍛えておくことが大事です。そして、グラフは「読み取る」だけでなく、「自分から積極的に描く」ことが、難問克服への一歩となることを心がけておきたいところです。
「1問目に注意!」 H28 第1回 1 (1)
2016/343時間に最も近いのは、(ア)時間(イ)分です。ア、イにあてはまる整数を答えなさい。
【解答解説】
こういう不安定要素の高い1問目から解き始め、ここで躓いてしまうと、その後も悪い流れが続いてしまい合格点を取ることが難しくなりますので、この手の問題は「一旦後回しにする」ことをおすすめいたします。
まず、分数2016/343をじっくり見つめ、冷静に判断することが重要です。分子と分母をそれぞれ素因数分解(素数の積に分解)すると、 2016=2×2×2×2×2×3×3×7 、343=7×7×7 以上より、元の分数は7で1回約分でき、2016/343=288/49となります。 よって、288/49=543/49= 6-6/49(時間)となり、さらに、60×6/49=717/49(分) となります。717/49(分)は四捨五入すれば7(分)となるので( 17/49< 1/2だから)、 求めるアは6-1=5(時間)、イは60-7=53(分)となります。
もちろん、まともに2016÷343のわり算の筆算をしてもできますが、仮に正解であったとしても、相手の揺さぶりペースに巻き込まれ、このあとも終始ペースを乱される可能性が高くなりますので、できるだけ「自分のペース」に引き込むためにも、とりあえず他の普通の問題から手を付け、当問題も工夫して解くべきです。
【まとめ】
以上のことから早稲田中学のような難関校の入試問題を解くというのは容易なことではないことがご理解いただけたかと思います。 この学校の算数入試問題の難易度が、ここ数年の間に格段に上がったことは明らかです。
また、毎年新傾向の問題を出題するだけでなく、「お約束のパターン問題」の設定を変え、不注意な受験生を引っかけるような問題も出題されます。
上述の通り「第1問に面倒な問題をもってくる」ことが多く、出題者の術中にはまらないためにも、ここを飛ばして試験後半に落ち着いて取り組むことが重要であると言えます。
繰り返しになりますが、早稲田中学では「図形(平面・立体)」分野を無視することはできません。過去問はもちろんのこと、どんな図形も応用レベルまで十二分に演習を積んで
おくことが肝要です。


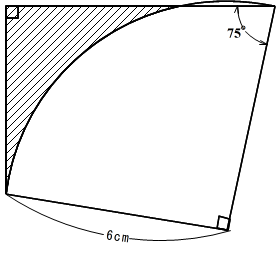




 図4,5,6
図4,5,6



